Exploring Fibonacci Formula in Python

Let’s explore many different methods and techniques for calculating the Fibonacci Series using Python.

The Fibonacci Series is beautiful, fascinating, mysterious! The series is defined as follows: every number is the sum of the two preceding ones. Simple:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

Calculating Fibonacci Iteratively

The simplest way to calculate a Fibonacci number (n) is simply to start at the beginning and work forwards, iteratively. This solution calculates all previous values, giving it an exponential running time — larger numbers take increasingly longer to calculate.

Calculating Fibonacci Recursively

The recursive approach to finding Fibonacci numbers is sometimes used as a teaching aid in computer science classes. You can see here that the function calls itself on line 14 — making it recursive.

This method works backwards from the starting position until it reaches either 1 or 0. Otherwise, it calculates the sum of all previous recursions.

Recursion works because the computer keeps track of where we are using a memory construct known as stack memory. This is limited! Trying to find large Fibonacci numbers would exhaust the stack space.

Also: the recursive algorithm suffers from the same time complexity problem as the iterative algorithm — it must calculate all of the values.

Using Memoization for Efficient Recursion

The previous recursive function is called repeatedly for some values of i. Instead of recalculating this value, we can use a technique known as memoization.

Memoization is simply taking note, or a memorandum, of the previous calculated output values. Then we return the memo instead of re-calculating the value.

Python supports memoization very nicely if we use a decorator function. The decorator wraps the algorithm, and intercepts all calls and all return values. By intercepting the calls and the return values, we can store them in a local cache — and in future use the cached answers.

We can now apply the memo decorator to our function fibonacci_wrapped and see a very large speed improvement. Unfortunately, recursion limits still apply.

Python has a built-in memoization decorator, the least recently used cache lru_cache:

@functools.lru_cache(maxsize=None)

We could save ourselves the trouble of writing our own (inefficient!) memoization decorator, and instead use the @functools.lru_cache. Don’t forget to import functools if you want to use this.

Using Matrix Multiplication to Calculate Fibonacci Numbers

The previous examples all suffered from the same problem: all preceding values in the sequence needed to be calculated. We can avoid this inefficiency by using matrix multiplication to directly compute the sequence’s value without calculating the predecessors.

You can read more about matrix multiplication here:

Because the Fibonacci sequence is linear and predictable, it can be efficiently calculated using linear algebra.

This formula requires a constant amount of memory space to complete, and takes linearly longer as the value of n increases.

Using the Golden Ratio to Calculate Fibonacci Numbers

This method is included for the sake of completeness!

The Fibonacci Sequence represents the golden ration perfectly, so we can use Binet’s formula to calculate it:

You can see that I’m cheating here. If the sequence number we’re searching for is higher than 71, this function silently cheats and instead uses the matrix multiplication method.

The Binet formula is precise algebra. However, computers must use an imprecise representation of floating-point numbers. As the values of n increase, the rounding errors also accumulate.

Using Bit Operations to Calculate Fibonacci

In an early article, I described some common formulae for performing bit arithmetic on integers. My long-time subscribers may have been wondering why, but now all is revealed!

It is important to have an understanding of binary arithmetic before we explore the following ways of calculating Fibonacci numbers.

The Lucas Sequence

In this treatment of Fibonacci numbers, I’d like to also show the Lucas Sequence. Like Fibonacci, Lucas numbers are the sum of their two predecessors — they just begin at a different place:

2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, ....

The Lucas numbers are therefore very closely related to Fibonacci numbers:

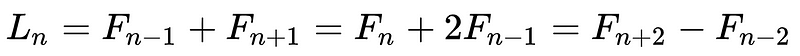
Let’s work with this with n=6 .

F(n-1) = F(5) = 3
F(n+1) = F(7) = 8
F(n-1) + F(n+1) = (3 + 8) = 11

L(6) = 11

Calculating Fibonacci Numbers with the Djikstra Formula

Edsgar Djikstra was perhaps the most brilliant theoretical computer science in modern history. He proposed an algorithm which uses the powers of the Lucas numbers to derive the related Fibonacci number.

Really quite brilliant. Here is the full algorithm:

The function fibonacci_djikstra recognisably uses the relationship between Lucas numbers and Fibonacci numbers I showed earlier: L(n) = F(n-1) + F(n+1).

It goes a step further, and uses the Lucas power function to exploit a part of Binet’s formula — see the integer 5 in there, and do you recognise that from the Golden Ration discussion?

For a more in-depth discussion of Djikstra’s algorithm, feel free to refer to this information.

Karatsuba Fast Multiplication

Following on from our discussion of binary arithmetic, there is one really interesting way to calculate very large products — Karatsuba multiplication.

According to Wikipedia, the Karatsuba algorithm was the first multiplication algorithm asymptotically faster than the quadratic “grade school” algorithm, it offers a speedup of 17.75 times versus the traditional quadratic formula for sufficiently large values.

We’ll use this algorithm in our next and final formula for calculating Fibonacci numbers!

Recursive Fast Doubling to Calculate Fibonacci

The following fast doubling formula uses four tools explained earlier: recursion, memoization, binary arithmetic and Karatsuba multiplication. You can guess why I chose to put this formula last!

This formula is very fast. It calculates Fibonacci to the 80'000 place in microseconds on my MacBook Pro.

I’ll explain how this works using the iterative variant, next.

Iterative Fast Doubling to Calculate Fibonacci

We can easily change the forms of an algorithm: from recursive to iterative or iterative to recursive. See how the following, iterative version of the previous differs:

It contains two loops. The first successively halves the sequence number we’re looking for. The second successively doubles it on the way back up. The iterative version is obviously slower but avoids overflowing the stack.

This algorithm uses an important property identified by number theorists: the “halving property”. It also vastly simplifies the matrix multiplication method by exploiting the formula:

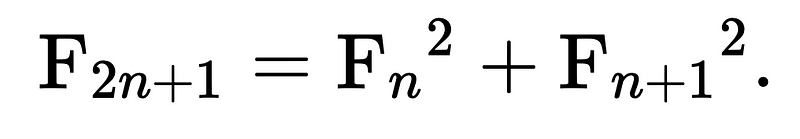
There are a lot of squares being calculated, which is where the Karatsuba multiplication is useful.

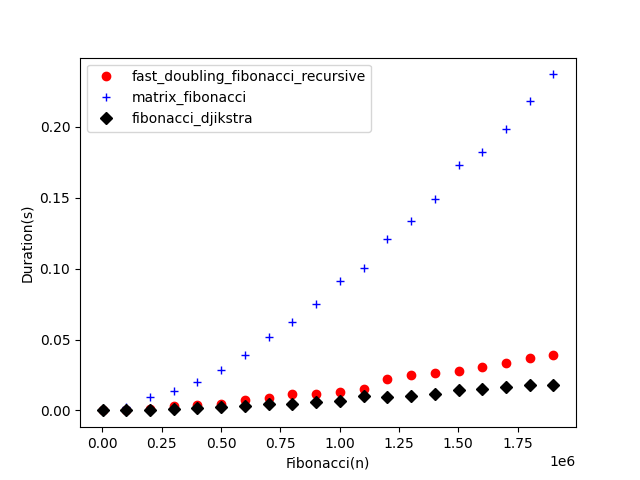
Timing Results

I thought you might be interested in the timing results. I decided to compare the matrix multiplication algorithm, the fast doubling algorithm, and the Djikstra algorithm. It’s pretty clear that the golden ratio, and the naive iterative and recursive algorithms will be slower.

Here is the code to collect the timing data:

And here is a graph of the timing results:

I hope you enjoyed this article! I’d like to invite you to follow me so that you can be notified when I publish the next article!