Learn Programming with Python — Introduction to Data Types: Numbers
Posted on May 03, 2020 in Learn Python
Learn Programming with Python — Introduction to Data Types: Numbers

Learn Programming with Python — Introduction to Data Types: Numbers
Numbers are everywhere! Learn how computer programmers use numbers without going totally crazy.
In the previous article, we explored
managing textual data using the str data type
in Python3. Now let’s move on to numbers. In this instalment we will spend most of our time
working on booleans, integers, floats and decimals. They are the most commonly used numerical
data types by computer programmers.
Numerical Data Types in Python
Numerical data can be managed in Python using the following data types:
intdata type contains integers, also called whole numbers, such1716booldata type contains Boolean values represented asTrueorFalsefloatdata type contains real numbers with a floating-point (decimal) such as3.14159decimalis a special data type in Python which we need to explicitly enable. It’s mainly used for working with monetary values.complexdata type contains complex numbers with a real and an imaginary part. Don’t worry if this makes no sense to you, I’m not exactly sure about it either! Python is used a lot in scientific circles, and those people sometimes need complex numbers. We won’t be discussing these again, ever :)
When to use the bool Data Type?
The bool data type is usually self explanatory! If
you want to store True or False, bool is for you! Thanks, George!
This is another very simple program which asks the user if they like anchovies:
After having run this a few times and made some different choices, my code editor looks like this:

The only time that the user input was evaluated as False is when no choice was made, I just pressed enter. Even when I entered the text “False”, Python evaluated this value to True.
Wait, what is going on here?
- On line 1 we define the variable
choiceusing the type hint:bool, Remember: this is a hint in Python, a hint to other programmers mainly! - We also execute the input() function we’ve seen before, asking the user a yes/no question. We tell the user that no input — just pressing enter — means no.
- We also force a type conversion
of the return value of
input()to abooldata type. We’ve seen this previously when we forced an age input to become an integer. Converting between one data type and another is also called a cast operation. - On line 2, we print the value of
choiceto the terminal — again making use of F-Strings.
As you can see, any text input,
whatsoever, is converted by the function bool()
to the value of True. Only the absence of any
input leads to False. Python is not doing any
super smart analysis to try to convert your “False”
statement to the bool value of False. Python doesn’t really speak a
natural language internally! If you have characters in a string, the conversion to a boolean
will result in True.
Programmers generally, and in Python particularly, love to use boolean values of either True or False as inputs to test conditions in If … Elif … Else constructs.
If we take the set of students from
earlier, we can convert a set to a bool too! If the set contains any elements at
all, the result of the conversion to a bool
will be True. If the set is empty, the
result will be False.
This is what it looks like after executing in my code editor:

What’s going on here?
- On lines 1 and 7 we define two
sets.
studentshas 3 elements butstockis empty. - On line 2 we convert
studentsto a bool value explicitly using thebool()function. - On lines 3 and 9 we are using the
len()built-in function to count the number of elements. Len takes a countable variable as its input, in our case we are passinglen()the entire set.len()is a very useful, built-in function. We can use it to count the number of characters in a string or the number of elements in any collection. - On line 7 we simply attempt to
coerce the value of
studentsinto aboolby passing it to the if test. We don’t need to explicitly convert tobool, like we did on line 2 because the intent is implicit! - Only if either of the sets
contains elements is the first if branch executed. Otherwise, the
elseclause is executed by default.
Don’t forget, we use curly brackets to indicate that we are creating a set — even an empty set!
We encountered the boolean operators
or, and,
and not in the previous article in this series.
Later we’ll explore using these operators for performing very fast calculations on large
numbers.
When to use the int Data Type?
The int data type is also a keen favourite of most programmers! It’s super-simple: it represents whole numbers — countable things. Programmers do a lot of counting in their programs. If our program needs to do calculations, or any other kind of analysis, integers are usually not the best choice because they can’t be used to represent fractions of a whole number. Integers are fine for simple addition (counting!) or subtraction.
In the following program, we’ll create a
str data type, and use a fairly awkward
construct for counting the number of vowels {a, e, i, o, u} in the string. Without looking
ahead, how would you do it using the concepts we’ve explored already?
This is how it looks in my code editor after executing the program.
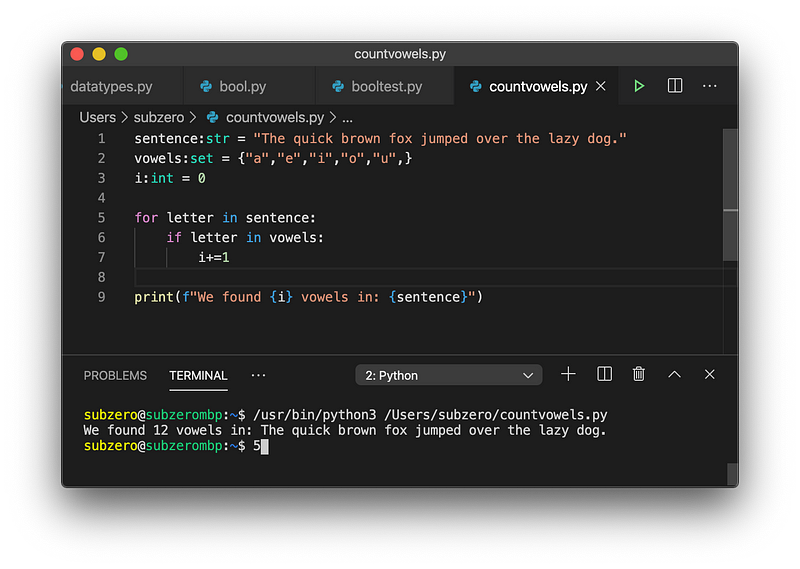
What’s going on here?
- On line 1 we create the variable
sentence, and use the type hint:strto indicate we intend to use this for storing a string. Then we assign a mildly amusing text to it. - On line 2 we create a set of vowels.
- On line 3 we create the variable
i, identify our intention to store an integer value, and also immediately give it the initial value of 0. - On line 5 we use the
foroperator to loop over every element insentence— each element is assigned toletteron each pass. - On line 6 we evaluate each
letterto see if it is contained in the set calledvowel. - On line 7, the test has evaluated
to True, so we increment our
counter,
i, by one. - On line 9 we print what we’ve found.
If you found this too easy — well done! You’re well on your way to becoming a Python programmer! Now see if you can decode how the following program works ;)
sentence:str = "The quick brown fox jumped over the lazy dog."
vowels:set = {"a","e","i","o","u",}
i:int = len([letter for letter in sentence if letter in vowels])
print(f"We found {i} vowels in: {sentence}")
This should bamboozle you! It was mean of me. Sorry. This uses a very common Python technique called list comprehension — which we’ll be exploring soon!
All of the basic mathematical operations work on integers: addition, subtraction, multiplication and division. Python also offers additional built-in operators for numbers, explained in full on the Python documentation website.
Unlike the str data types, Python doesn’t offer a great variety of built-in functions for numbers. The reason is that numbers are primarily used in mathematical operations, there is not much else that can be done with them.
When to use the float Data Type?
The float data type is used for real numbers with floating point precision. This means that these numbers can become very precise — with very many numbers following the decimal point. The constant pi can be stored in a float, for example, 11.635468468471303.
Floats are often used when working with calculations which return fractions (such as division):
>>> print(type(3/4))
<class 'float'>
Although we were using only the integers 3 and 4, Python3 returns a float when performing division on integers. This is true whether or not the result is a decimal fraction or a whole number:
>>> print (type(10/20))
<class 'float'>
Programmers who wish to work with integers as the result of a division in Python3 have two choices: 1) convert the result to an integer or 2) use floor division using the // operator:
print (type(int(10/20)))
<class 'int'>
print (type(3//4))
<class 'int'>
Floor division always returns a whole
number — an int — and discards whatever the
remainder is.
When Not to Use the Float Data Type?
The float data type is a little bit imprecise. See the following program:
Here is the output in my code editor:

What’s going on here?
- On line 1 we create a variable
value, hint that we expect this to be afloat, and assign it the value 0.0 - On line 3 I’ve sneakily
introduced a new built-in function:
range(). Instead of looping over a predefined set as we did earlier, hererange(10)will create a sequence of integers from 1 to 10 for the for loop to work on. - On line 4 we use the
+=operator to increment the current value by 0.1 - On line 5 we print out the
current value during each iteration of the
forloop - On line 6 I’ve been blatant about
introducing yet another new built-in operator:
assert. Asserting that an expected condition exists, and otherwise creating an error conditionAssertionError:is a smart thing to do when programming! I gave myself extra points here because I also used a custom error message with the assert statement.
What we see in the program’s output is
that incrementing 0 by 0.1 a total of 10 times does not, as you would expect, give us a clean
1.0 as a result. We get a number which is ever-so-infinitesimally not 1.0: 0.9999999999999999. This may
not seem like a big deal, but pennies make pounds in the banking business! If you’d like to
understand more about why the float data type
must be imprecise, head over to this
resource and come back here to find out what we can do instead!
Why is this happening? Computers work on bits which are either 0 or 1. They don’t work on a bit size of 0…9. Computers don’t have 10 fingers, they have either on or off, 0 or 1, True or False. And so computers, hidden deeply, use the binary number system. Head over to Khan Academy for an introduction to binary numbers. Your computer has special circuitry in the processor to work with floating-point arithmetic, which uses the binary system. When we convert ⅓ to a decimal fraction we get an infinitely repeating representation: 0.3333333… because the decimal system can’t represent ⅓ precisely. Binary can’t really represent ⅒ either — it is imprecise in binary but not in decimal.
We can use rounding to get a less precise representation of this value:
In my code editor I get this output:
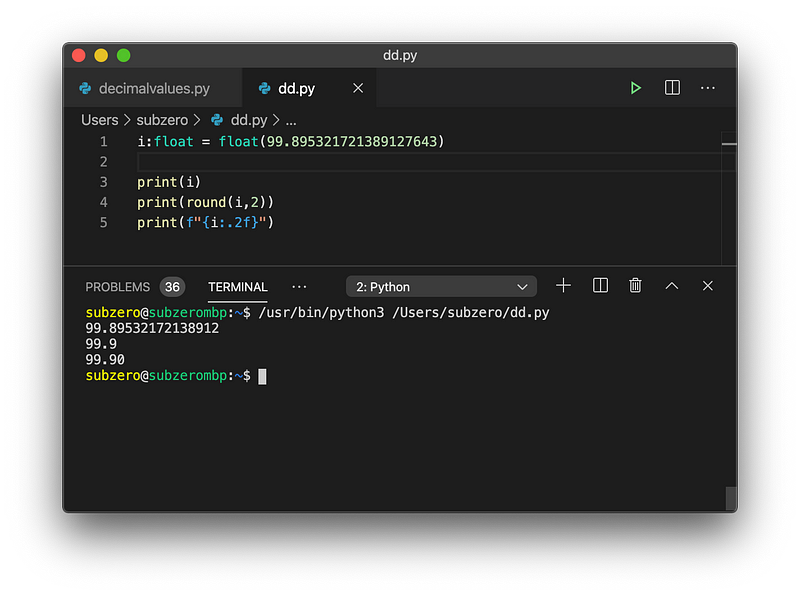
What’s going on here?
- On line 1 I define a variable
iwith the hint that I want to use afloat, and then I assign a very precise value toi. - On line 3 I print
iand see that it has been truncated to a less precise value by Python. - On line 4 I use the built-in
round() function, passing two arguments:
iand the desired precision of 2 decimal places. To Python, 99.9 is just as precise 99.90. - On line 5, inside my F-String, I
indicate that the output should specially format the value of
iusing the formatting specifier:.2f. This means, after the decimal place, two numerical values. A full list of formatting specifiers can be found in the Python docs.
It is very easy to display a float using less precision than it contains internally.
When to use the Decimal Data Type
If we want to be precise when using decimal fractions, as when working with monetary values, Python can help — but we programmers have to do a little bit of work. We need to go beyond the default capability of Python and use an extra set of functionality contained in a module. Python modules provide power-ups, a new set of capabilities. Most programmers don’t need to work precisely with decimals every day. Python offers us the ability to use decimal values but expects that we know what we’re doing and why. Luckily, we do (or at least, you do)!
The following program is functionally a
repeat of the program shown earlier, except here we are using the decimal data type.
In my editor, I get the following output:

What’s going on here?
- On line 1, I am using the import
statement to add the entire contents of the
decimalmodule using the*wildcard. - On line 3, I instruct the decimal
library to use the
BasicContext— which makes it use a precision of 6 significant digits. - On lines 4 and 7 I am being
explicit in saying that the values used should be of the
decimaldata type. Otherwise, Python would default tofloat.
You may notice that my editor is
showing 36 problems and a wavy underline underneath from.
This is because I’m importing an entire module using *, although I’m only using a small part of
it. This is considered bad practise, we’ll get around to discussing how to avoid this problem in
future.
Order of Operations in Python
You may remember from school math about a concept called “order of operations”. Python uses the PEMDAS method (parenthesis, exponents, multiplication and division, addition and subtraction). In some countries, the same concept is called BODMAS (brackets, order, multiplication and division, addition and subtraction). They mean the same thing, the difference is mainly caused by different English speaking countries using alternative synonyms. The following example shows that you’ve probably been taught to do multiplications and divisions before additions and subtractions:
12 * 2 + 5 = 29
12 + 2 * 5 = 22
If you need a refresher, Wikipedia has a great simple English page on the topic. So far so good, but always remember the order! Work from left to right. Both multiplication and division have equal precedence, as do both addition and subtraction:
10 / 2 * 5 = 25
10 - 3 + 5 = 12
8 / 4 * 5 = 10
If you don’t agree, try these examples out using Python. Trust me and thousands of scientists — Python gets it right!
What have we Achieved?
- We’ve looked at the
bool,int,floatanddecimalnumerical data types in Python3. - Performed type conversions from one data type to another.
- We saw the
len()built-in function which returns the number of elements in a sequence. - You got a first taste of using list comprehensions in Python.
- We saw that performing a division
on two integers results in a value with data type
float. We also saw that the mathematical operator//(floor division) returns an integer with no remainder. - I introduced the
range()built-in function to you. When used as the sequence in a for loop, it can allow us to loop a fixed number of times. - We briefly touched on using the
assertstatement during programming to ensure that our program is operating as intended. - We examined how the
floatdata type is inherently imprecise and doesn’t behave quite as you’d expect. - We looked at using
round()and at using format specifiers to display afloatwith less precision. - We introduced the
decimalmodule, which extends Python3’s capabilities — when needed — to cover the kind of precision needed when working with currency. - We looked at the PEMDAS order of evaluation when working with calculations.
We have covered a lot of ground here,
and so far in this series, you’ve seen most of the basic building blocks used by programmers
every day. In the next article in this series, we’ll extend our knowledge of how Python3 manages
sequences of data — beyond the set and tuple which we have already got to grips
with. We’ll move on to understanding the list
compound data type in Python3, amongst others.
Articles in this series so far:
- Learn Programming with Python — An Introduction
- Learn Programming with Python — Introduction to Functions
- Learn Programming with Python — Controlling Execution Flow
- Learn Programming with Python — Introduction to Data Types: Strings
- Learn Programming with Python — Introduction to Data Types: Numbers
- Learn Programming with Python — Introduction to Compound Data Types: Sets and Tuples
- Learn Programming with Python — Introduction to Compound Data Types: Lists
- Learn Programming with Python — Introduction to Compound Data Types: Dictionaries
A note from Python In Plain English
We are always interested in helping to promote quality content. If you have an article that you would like to submit to any of our publications, send us an email at submissions@plainenglish.io with your Medium username and we will get you added as a writer.